[js]サイズに合わせた画像の縮小

画像を任意のサイズに縮小するときの計算方法について説明します。
ソースコードにはJavascriptを使っていますが、なるべく言語に依存しないようにするつもりです。

この手の計算は、寄り付かない人には、ものすごく苦手意識があるのではないかと想像します。
落ち着けば、大変な計算はぜんぜん出てきません。
また、理屈を簡潔に語るよりも、計算から感覚的にイメージがつかめるほうがよいと思ったので、わりとくどくど説明しています。

画像を任意のサイズに合わせる

画像を任意の矩形サイズに合わせたいとします。
やってくる画像のサイズはまちまちですが、なるべく画像の全容が見えるようにして、収まらない部分は切り落としてしまうことにします。

当然ですが、幅と高さにサイズを指定して、強引にギュッとゆがめてしまうのは画像にもよろしくありません（変倍というやつです）。
幅と高さは同じ比率（等倍）で収めるものとします。

横長画像か縦長画像かを判定する

画像によって、処理の仕方は2パターンあります。
横長の画像は左右が余るようにしたいですし、縦長の画像は上下を余るようにしたいですね。

具体的な数をもとに考えることができるように、例として、フラミンゴの画像とヒマワリの画像を使います。
それぞれの画像サイズはこちら。

		幅	高さ
A	フラミンゴの画像	450px	300px
B	ヒマワリの画像	400px	400px
描画先の矩形サイズ		100px	80px

フラミンゴの画像とヒマワリの画像を、描画先の矩形サイズに合わせて縮小したいとします。

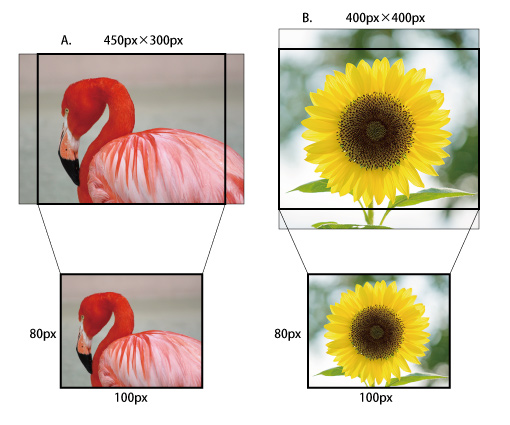
それぞれの縦横の比率を比較することで、どちらに合わせる画像かを判別させます。

フラミンゴの縦横比率（幅／高さ）= 450px / 300px = 3/2 = 1.5
ヒマワリの縦横比率（幅／高さ）= 400px / 400px = 1.0
描画先の矩形の縦横比率（幅／高さ）= 100px / 80px = 5/4 = 1.2

縦横比率の関係は、
フラミンゴ（1.5） 　＞　描画先の矩形（1.2）　＞　ヒマワリ（1.0）
となっています。

描画先の矩形よりも縦横比率が大きいものは横長として扱えばよく、小さいものは縦長として扱えばよいことが解りますね。

切り出す画像と縮小率を計算する

必要となるのは、画像のどの部分を切り出して、どのくらい縮小すればいいかという2つです。
ひとまず横長画像について考えます。

先に縮小比を求める

どのくらい小さく（または大きく）すればいいのかを考えます。

横長の画像は左右に余りますので、画像の高さを、描画先の矩形の高さに合わせると考えると解りやすいですね。

縮小比 = 描画先の矩形の高さ ／ 画像の高さ
です。

※縮小と書いていますが、計算式には縮小と拡大の区別はありません。画像が小さくて、描画先の矩形のほうが大きいときは、縮小比が1よりも大きくなるだけですね。

切り取り領域を決める

画像から領域を切り取り、縮小することで、描画先の矩形に合わせます。
どの部分の領域を切り取ればいいかを求めます。

・高さ
高さはそのまま、画像の高さを描画先の矩形の高さにするだけです。

切り取る領域の高さ = 画像の高さ

・幅
幅について考えます。
切り取る領域の幅に縮小比を掛ければ描画先の矩形の幅になるはずなので、切り出し幅を求めるためには逆に縮小比で割ってあげればよいでしょう。

描画先の矩形の幅 = 切り取る領域の幅×縮小比
なので、
切り取る領域の幅 = 描画先の矩形の幅／縮小比
で計算できます。

・切り取りの開始位置
また切り取りの開始位置は横幅の画像は左右に余る分を、少しずらせばいいことが判ります。
画像の幅と切り取り幅の差分があまりの部分ですので、真ん中の部分を切り取るためには、差分を等分すればよいですね。

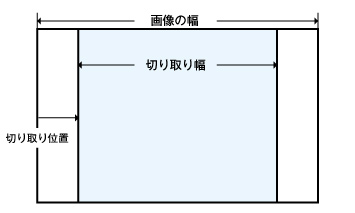
ということで、
切り取りの開始位置 = (画像の幅 - 切り取り幅) / 2
で計算できます。

縦長の画像のときの計算

縦長の画像も同じように計算しましょう。
縦長の画像の場合は、縮小比は幅の比率になります。

縮小比 = 描画先の矩形の幅 / 画像の幅

・幅
切り取る領域の幅 = 画像の幅

・高さ
切り取る領域の高さ = 描画先の矩形の高さ／縮小比

・開始位置
開始位置は、上下の位置を決めます。
縦の切り取りの開始位置 = (画像の幅 - 切り取る高さ) / 2
で計算できます。

ソースコード

サンプルとして、画像をロードし、幅250px、高さ100pxに合わせて縮小するソースコードを載せておきます。
なお、言語はJavascriptです。
html内にcanvasのidを持つcanvasタグが配置されているものとします。

var imageFile = "/Images/ヒマワリ.jpg";
var id = "canvas"
var canvasWidth = 250;
var canvasHeight = 100;

var canvas = document.getElementById(id);
canvas.width = canvasWidth;
canvas.height = canvasHeight;
var context = canvas.getContext('2d');

var image = document.createElement('img');
image.src = imageFile;

// 準備
image.onload = function () {
    var imageWidth = image.width;
    var imageHeight = image.height;

    // ①縮小比を計算
    var scale = 1.0;
    if (imageWidth / imageHeight > canvasWidth / canvasHeight) {
        scale = canvasHeight / imageHeight;
    } else {
        scale = canvasWidth / imageWidth;
    }

    // ②切り出し領域を計算
    var clipWidth = canvasWidth / scale;
    var clipHeight = canvasHeight / scale;
    var clipX = (imageWidth - clipWidth) / 2;
    var clipY = (imageHeight - clipHeight) / 2;
　　
    // ③drawImageメソッドの呼び出し
    context.drawImage(image, clipX, clipY, clipWidth, clipHeight, 0, 0, canvasWidth, canvasHeight);

};

解説

計算に使っている変数をざっとリストアップしておきます。

imageWidth	画像のオリジナルサイズの幅
imageHeight	画像のオリジナルサイズの高さ
canvasWidth	指定矩形の幅
canvasHeight	指定矩形の高さ
scale	縮小比
clipX	切り取り領域の開始X座標
clipY	切り取り領域の開始Y座標
clipWidth	切り取り領域の幅
clipHeight	切り取り領域の高さ

準備として、画像を読み込んでから処理されるようにしたいのでonloadイベントに記述しています。

①縮小比を計算

縦横比率を比較し、横長の画像と、縦長の画像に分けて縮小比率を計算しています。

※
完全に横道にそれますが、割り算は掛け算に比べてものすごく遅いです。
(imageWidth / imageHeight > canvasWidth / canvasHeight)
は、下のようにも書けます。
(imageWidth * canvasHeight > imageHeight * canvasWidth)
こちらのほうが高速です。

②切り出し領域を計算

画像の切り出し領域を計算しています。
横長でも縦長でも縮小比が解れば同じ計算式で導くことができます。

※
ただし不要な演算が増えているので注意。

③drawImageメソッドの呼び出し

canvasのdrawImageメソッドを呼び出しています。
drawImageは、canvasにイメージを描画するためのメソッドです。
drawImageは引数の多い9つあるのを使っています。

context.drawImage(image, sx, sy, sw, sh, dx, dy, dw, dh)

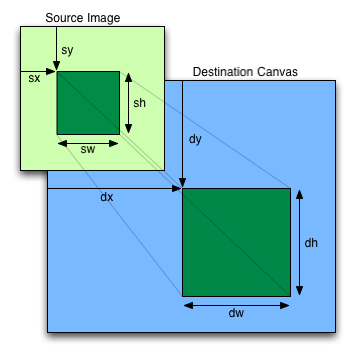
sx,sy,sw,shで描画元からコピーする矩形を指定し、dx,dy,dw,dhで描画先の矩形を指定します。


以上で終わりですが、もう一つだけ足しておきます。

おまけ

上記は、できるだけ画像を矩形いっぱいに広げて収めるという要件でした。
そのため矩形よりもはみ出た領域は切り取られてしまいます。

替わりに、画像を切り取ることなく、画像の全体を矩形に表示したいとします。
こういうのもありそうな話です。

こういう感じですね。

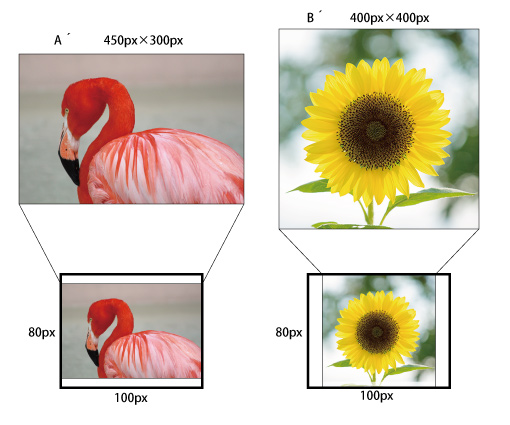
横長画像か縦長画像かを判定するために縦横比率を比較しました。
この判定を反転させます。

上のソースコードでいうと、
if (imageWidth / imageHeight > canvasWidth / canvasHeight) {
を
if (imageWidth / imageHeight < canvasWidth / canvasHeight) {
にする。
するとあら不思議。

幅と高さのどちらを基準にサイズを合わせるか、というのを逆転させればよいので、これだけでできるのです。


おしまい。